Question

Which expressions are polynomials?

Answer 1

Option A: z + 1

Option B: 6 + w

Option D:
`2 x^(4)-y`

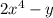
Solution:

Let us first define the polynomial.

A polynomial can have constants, variables, exponents and fractional coefficients.

A polynomial cannot have negative exponents, fractional exponents and never divided by a variable.

To find which expressions are polynomial:

Option A: z + 1

By the definition, z + 1 is a polynomial.

It is polynomial.

Option B: 6 + w

By the definition, 6 + w is a polynomial.

It is polynomial.

Option C:
`y^(2)-\sqrt[3]{y}+4`

`y^(2)-\sqrt[3]{y}+4=y^(2)-{y}^(1/3)+4`

Here, y have fractional exponent.

So, it is not a polynomial.

Option D:
`2 x^(4)-y`

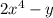
By the definition,
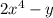`2 x^(4)-y` is a polynomial.

It is polynomial.

Hence z + 1, 6 +w and
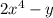`2 x^(4)-y` are polynomials.