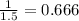Question

refractive index of Glass sample is 1.52 and date of Ruby is 1.71 if the speed of light in vacuum b 3 into 10 to the power 8 metre per second find the speed of light in glass in Ruby and also calculate the refractive index of air with respect to glass​

Answer 1

The speed of light in glass
`1.97 * 10^(8)\ \mathrm{m} / \mathrm{s}`

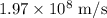
The speed of light in Ruby is
`1.75 * 10^(8) \mathrm{m} / \mathrm{s}`

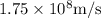
The refractive index of air with respect to glass​ is 0.666

Step-by-step explanation:

The refractive index is the degree of diffraction of a light beam passing from one medium to another. It can also be defined as the ratio of the speed of light in an empty space to the speed of light in a material. The equation is given as

`\text {refractive index, n\ or } \mu=\frac{\text c}{\text {v}}`

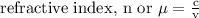
Given data:

`\mu_{\text {glass}}=1.52`

`\mu_(r u b y)=1.71`

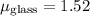
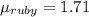
Velocity of light in vacuum, c =
`3 * 10^(8) \mathrm{m} / \mathrm{s}`

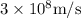
We need to find velocity of glass, ruby and refractive index ratio of air and glass

To find velocity of glass,

`1.52=\frac{3 * 10^(8)}{\text {velocity of glass}}`

`\text {velocity of glass}=(3 * 10^(8))/(1.52)=1.97 * 10^(8) \mathrm{m} / \mathrm{s}`

To find velocity of ruby,

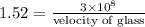
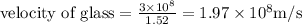
`1.71=\frac{3 * 10^(8)}{\text {velocity of Ruby}}`

`\text {velocity of Ruby}=(3 * 10^(8))/(1.71)=1.75 * 10^(8)\ \mathrm{m} / \mathrm{s}`

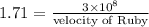
To calculate the refractive index of air with respect to glass: =
`\frac{\mathrm{n}_{\text {air}}}{\mathrm{n}_{\text {glass}}}`

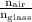
We know, the value of the refractive index of air is 1

The value of the refractive index of glass is 1.5

So, the ratio of them should be
`(1)/(1.5)=0.666`