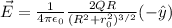Question

A ring of charge of radius r0 lies in the x-y plane with its center at the origin.The charge counterclockwise from θ = 0º to θ = 180º is uniformly distributed with the total charge equaling Q. The charge counterclockwise from θ = 180º to θ = 360º is uniformly distributed with the total charge for this half of the ring equaling –Q. What is the direction of the electric field on the z-axis at the position (x, y, z) = (0, 0, ​r0)?

Answer 1

`\vec{E} = (1)/(4\pi\epsilon_0)(2QR)/((R^2 + r_0^2)^(3/2))(-\^y)`

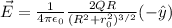
The direction of the electric field is in the negative y-direction.

Step-by-step explanation:

We will separate the both halves of the ring and calculate the E-field separately. We will use the following formula and the method of integration.

`\vec{E} = (1)/(4\pi\epsilon_0)(Q)/(r^2)\^r`

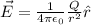
We will choose an arbitrary infinitesimal displacement (ds) on the ring. We will apply the above formula to that small segment, then integrate over the half ring.

The small segment has a length ds. This segment is also equal to Rdθ, because any curve on the ring is equal to radius times angle, and the angle of the infinitesimal displacement is the smallest angle we could choose, dθ.

`dE = (1)/(4\pi\epsilon_0)(dQ)/(R^2 + r_0^2)`

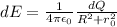
dQ can be written in terms of given variables according to the fact that the charge density of the total ring is equal to any small segment of the ring.

`(Q)/(\pi R) = (dQ)/(Rd\theta)\\dQ = (Qd\theta)/(\pi)`

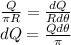
dE becomes,

`dE = (1)/(4\pi\epsilon_0)(Qd\theta)/(\pi)(1)/(R^2 + r_0^2)`

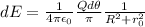
Before integrating this quantity, we have consider the fact that electric field is a vector, therefore has to be separated into its vertical and horizontal components.

`dE_v = dEsin(\alpha) = dE (r_0)/(√(R^2 + r_0^2))\\dE_h = dEcos(\alpha) = dE (R)/(√(R^2 + r_0^2))`

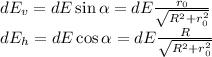
These equalities can be deduced from the geometry of the ring.

Now, we can conclude our method by integrating both halves.

`E_1_(v) = \int\limits^(\pi)_0 {dE_1_(v)} \, d\theta = \int\limits^(\pi)_0 {(1)/(4\pi\epsilon_0)(Q)/(\pi)(r_0)/((R^2 + r_0^2)^(3/2)) \, d\theta = (1)/(4\pi\epsilon_0)(Q)/(\pi)(r_0)/((R^2 + r_0^2)^(3/2))\int\limits^(\pi)_0 \, d\theta = (1)/(4\pi\epsilon_0)(Q)/(\pi)(r_0)/((R^2 + r_0^2)^(3/2)) \pi`
`E_1_(v) = (1)/(4\pi\epsilon_0)(Qr_0)/((R^2 + r_0^2)^(3/2))\^z`

`E_1_(h) = \int\limits^(\pi)_0 {dE_1_(h)} \, d\theta = \int\limits^(\pi)_0 {(1)/(4\pi\epsilon_0)(Q)/(\pi)(R)/((R^2 + r_0^2)^(3/2)) \, d\theta = (1)/(4\pi\epsilon_0)(Q)/(\pi)(R)/((R^2 + r_0^2)^(3/2))\int\limits^(\pi)_0 \, d\theta = (1)/(4\pi\epsilon_0)(Q)/(\pi)(R)/((R^2 + r_0^2)^(3/2)) \pi`
`E_1_(h) = (1)/(4\pi\epsilon_0)(QR)/((R^2 + r_0^2)^(3/2))(-\^y)`

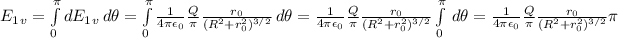
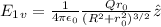
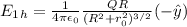
We will repeat these calculations for the bottom half of the ring:

`E_2_(v) = \int\limits^(\pi)_0 {dE_2_(v)} \, d\theta = \int\limits^(\pi)_0 {(1)/(4\pi\epsilon_0)(-Q)/(\pi)(r_0)/((R^2 + r_0^2)^(3/2)) \, d\theta = (1)/(4\pi\epsilon_0)(-Q)/(\pi)(r_0)/((R^2 + r_0^2)^(3/2))\int\limits^(\pi)_0 \, d\theta = (1)/(4\pi\epsilon_0)(-Q)/(\pi)(r_0)/((R^2 + r_0^2)^(3/2)) \pi`
`E_2_(v) = (1)/(4\pi\epsilon_0)(Qr_0)/((R^2 + r_0^2)^(3/2))(-\^z)`

`E_2_(h) = \int\limits^(\pi)_0 {dE_2_(h)} \, d\theta = \int\limits^(\pi)_0 {(1)/(4\pi\epsilon_0)(-Q)/(\pi)(R)/((R^2 + r_0^2)^(3/2)) \, d\theta = (1)/(4\pi\epsilon_0)(-Q)/(\pi)(R)/((R^2 + r_0^2)^(3/2))\int\limits^(\pi)_0 \, d\theta = (1)/(4\pi\epsilon_0)(-Q)/(\pi)(R)/((R^2 + r_0^2)^(3/2)) \pi`
`E_2_(h) = (1)/(4\pi\epsilon_0)(QR)/((R^2 + r_0^2)^(3/2))(-\^y)`

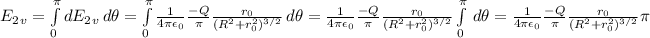
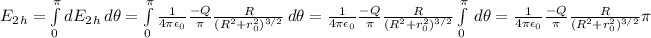
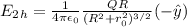
Therefore, the net electric field created by the ring is the sum of these four components. Note that the vertical components cancel out each other.

`\vec{E} = (1)/(4\pi\epsilon_0)(2QR)/((R^2 + r_0^2)^(3/2))(-\^y)`