Step-by-step explanation:
As the force is given as 5.30 kN or
 . Hence, mass will be calculated as follows.
. Hence, mass will be calculated as follows.
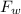 = mg
= mg
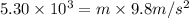
m = 540.816 kg
(a) At the top, centripetal force
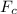 is acting upwards and the weight of the riders and car,
is acting upwards and the weight of the riders and car,
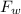 will be acting downwards.
will be acting downwards.
Therefore, force on the car by the boom will be calculated as follows.

or,

=
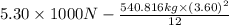
= 4715.919 N
Hence, the force
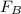 on the car from the boom is 4715.919 N. This means that the car will be hanging on the boom and the boom will exert an upward force.
on the car from the boom is 4715.919 N. This means that the car will be hanging on the boom and the boom will exert an upward force.
(b) Now at the top, centripetal force
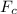 will be acting upwards and the weight of cars and car riders will be acting in the downwards direction.
will be acting upwards and the weight of cars and car riders will be acting in the downwards direction.
Hence, we will calculate the force on car by the boom as follows.

or,

=
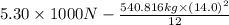
= -3533.33 N
Therefore, car will be pushing on the boom and the boom will exert a downward force.