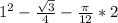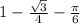Question

Suppose a square ABCD has a side length of 1 unit. The arcs BD and AC are circular arcs with centers at A and D, respectively. Find the area of the shaded region.

Answer 1

`1-(√(3) )/(4)-(\pi)/(6)`

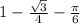
Explanation:

The missing figure is shown in the attachment

The area of the shaded region = Area of Square - (Area of sector AOB + Area of equilateral triangle BOC + Area of sector COD)

Area of Sector AOB=Area of Sector COD=
`(30)/(360)*\pi*1^2=(\pi)/(12)`

Area of equilateral triangle =
`(1)/(2)*r*(√(3) )/(2)*r= (1)/(2)*1*(√(3) )/(2)*=(√(3) )/(4)`

Area of shade region =
`1^2-(√(3) )/(4)-(\pi)/(12)*2`

`1-(√(3) )/(4)-(\pi)/(6)`