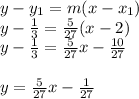Answer:
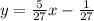
Explanation:

To find slope of f(x) at x=2, find the derivative f'(x)
apply quotient rule to find derivative
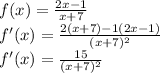
f'(x) is the slope . Now find slope at x=2. plug in 2 for x
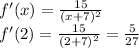
find out f(x) when x=2
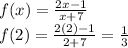
Now frame the equation of the line
(2,1/3) slope = 5/27