Question

Three students were applying to the same graduate school. They came from schools with different grading systems. Student GPA School Average GPA School Standard Deviation Thuy 2.7 3.2 0.8 Vichet 88 75 20 Kamala 8.8 8 0.4 Which student had the best GPA when compared to other students at his school? Explain how you determined your answer. (Enter your standard deviation to two decimal places.) had the best GPA compared to other students at his school, since his GPA is standard deviations

Answer 1

Kamala had the best GPA compared to other students at his school, since his GPA is 2 standard deviations above his school's mean.

Explanation:

The z-score measures how many standard deviation a score X is above or below the mean.

it is given by the following formula:

`Z = (X - \mu)/(\sigma)`

In which

`\mu` is the mean,
`\sigma` is the standard deviation.

In this problem:

The student with the best GPA compared to other students at his school is the one with the higher z-score, that is, the one whose grade is the most standard deviations above the mean for his school

Thuy

Student GPA| School Average GPA| School Standard Deviation

Thuy 2.7| 3.2| 0.8

So
`X = 2.7, \mu = 3.2, \sigma = 0.8`

`Z = (X - \mu)/(\sigma)`

`Z = (2.7 - 3.2)/(0.8)`

`Z = -0.625`

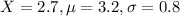
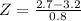
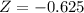
Thuy's score is -0.625 standard deviations below his school mean.

Vichet

Student GPA| School Average GPA| School Standard Deviation

Vichet 88| 75| 20

So
`X = 88, \mu = 75, \sigma = 20`

`Z = (X - \mu)/(\sigma)`

`Z = (88 - 75)/(20)`

`Z = 0.65`

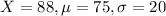
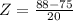
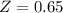
Vichet's score is 0.65 standard deviation above his school mean

Kamala

Student GPA| School Average GPA| School Standard Deviation

Kamala 8.8| 8| 0.4

So
`X = 8.8, \mu = 8, \sigma = 0.4`

`Z = (X - \mu)/(\sigma)`

`Z = (8.8 - 8)/(0.4)`

`Z = 2`

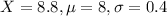
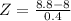
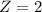
Kamala's score is 2 standard deviations above his school mean.

Kamala has the higher z-score, so he had the best GPA when compared to other students at his school.

The correct answer is:

Kamala had the best GPA compared to other students at his school, since his GPA is 2 standard deviations above his school's mean.