Question

Suppose that the mean water hardness of lakes in Kansas is 425 mg/L and these values tend to follow a normal distribution. A limnologist would like to know whether stock ponds tend to have lower hardness. He collected water from 25 randomly-selected stock ponds, which yielded the following results. Test the appropriate null hypothesis. 346 496 352 378 315 420 485 446 479 422 494 289 436 516 615 491 360 385 500 558 381 303 434 562 496

Answer 1

The mean water hardness of lakes in Kansas is 425 mg/L or greater.

Explanation:

We are given the following data set:

346, 496, 352, 378, 315, 420, 485, 446, 479, 422, 494, 289, 436, 516, 615, 491, 360, 385, 500, 558, 381, 303, 434, 562, 496

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

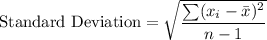
where
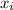`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(10959)/(25) =438.36`

Sum of squares of differences = 175413.76

`S.D = \sqrt{(175413.76)/(24)} = 85.49`

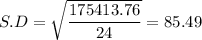
Population mean, μ = 425 mg/L

Sample mean,
`\bar{x}` = 438.36

Sample size, n = 25

Alpha, α = 0.05

Sample standard deviation, s = 85.49

First, we design the null and the alternate hypothesis

`H_(0): \mu \geq 425\text{ mg per Litre}\\H_A: \mu < 425\text{ mg per Litre}`

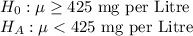
We use one-tailed t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(s)/(√(n)) }`

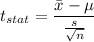
Putting all the values, we have

`t_(stat) = \displaystyle(438.36 - 425)/((85.49)/(√(25)) ) = 0.7813`

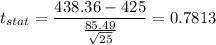
Now,
`t_(critical) \text{ at 0.05 level of significance, 24 degree of freedom } = -1.7108`

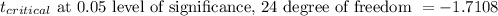
Since,

The calculated t-statistic is greater than the critical value, we fail to reject the null hypothesis and accept it.

Thus, the mean water hardness of lakes in Kansas is 425 mg/L or greater.