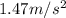Question

A worker pushes a 200-N box (weight of box, you have to find mass) resting on a level floor with a force of 30 N. What is the acceleration (in m/s^2) of the block if the floor has negligible friction?

Answer 1

For the problem we will apply the concepts related to Newton's second law. Recall that this is defined as the product between mass and acceleration, and that in special cases, when the acceleration is equivalent to the force of gravity, the force is equivalent to the weight of the person. From these relationships we will find the mass, and then the acceleration with the given force.

`F_w = mg`

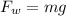
Here,

`F_w`= Force

m = Mass

g = Gravity

Replacing and rearranging we have that the mass is,

`m = (F_w)/(g) = (200)/(9.81)`

`m = 20.387kg`

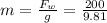
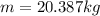
Now using the value of the force, but solving for the acceleration with the previous value of the mass we have,

`F = 30N`

`a = (F)/(m)`

`a = (30)/(20.387)`

`a = 1.47m/s^2`

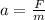
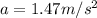
Therefore the acceleration of the box is
`1.47m/s^2`