Question

asked Sep 23, 2021 108k views

1 Answer

Ktretyak · Answer 1 · 2021-09-28T18:52:44+0000

Answer:

a) 15.63% probability that 5 hits are received in a given minute.

b) 6.88% probability that 9 hits are received in 1.5 minutes.

c) 67.67% probability that fewer than 3 hits are received in a period of 30 seconds.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

In which

x is the number of sucesses

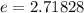e = 2.71828 is the Euler number

$\mu$ is the mean in the given time interval.

(a.) What is the probability that 5 hits are received in a given minute?

Mean rate of 4 per minute, which means that
$\mu = 4$

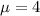
This is P(X = 5).

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

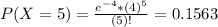
P(X = 5) = (e^(-4)*(4)^(5))/((5)!) = 0.1563

15.63% probability that 5 hits are received in a given minute.

(b.) What is the probability that 9 hits are received in 1.5 minutes?

Mean rate of 4 per minute, so for 1.5 minutes,
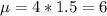
$\mu = 4*1.5 = 6$

This is P(X = 9).

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

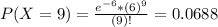
P(X = 9) = (e^(-6)*(6)^(9))/((9)!) = 0.0688

6.88% probability that 9 hits are received in 1.5 minutes.

(c.) What is the probability that fewer than 3 hits are received in a period of 30 seconds?

Mean rate of 4 per minute, so for 30 seconds = 0.5 minutes,
$\mu = 4*0.5 = 2$

This is

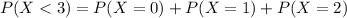
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)

In which

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

P(X = 0) = (e^(-2)*(2)^(0))/((0)!) = 0.1353

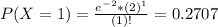
P(X = 1) = (e^(-2)*(2)^(1))/((1)!) = 0.2707

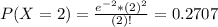
P(X = 2) = (e^(-2)*(2)^(2))/((2)!) = 0.2707

So

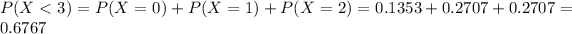
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.1353 + 0.2707 + 0.2707 = 0.6767

67.67% probability that fewer than 3 hits are received in a period of 30 seconds.

Please log in or register to add a comment.