Answer:
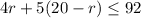
=======================================
Step-by-step explanation:
r = number of red pens
4r = cost of buying r red pens
example: if r = 10, then 4r = 4*10 = 40 is the total cost of buying 10 red pens
If John buys r red pens, then he must buy 20-r black pens so that r and 20-r add to 20.
John buys 20-r black pens, and at $5 each, so it will cost 5(20-r) dollars for just the black pens alone.
In total, John spends 4r + 5(20-r) dollars for all the pens (red & black)
We want $92 be the most he spends. This is the ceiling or highest value possible.
Therefore,
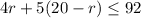
--------------------
Extra info:
If you want to solve for r, then
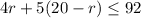
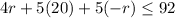 distribute
distribute
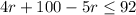
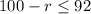
 add r to both sides
add r to both sides
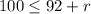
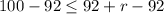 subtract 92 from both sides
subtract 92 from both sides
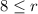
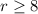
So John must buy at least 8 red pens. The most he can buy is 20 red pens since he wants 20 pens total.