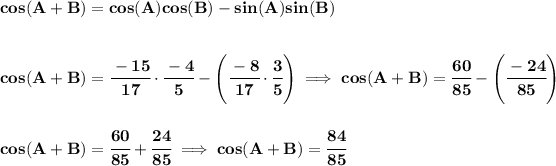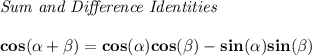
we know that angle A is in the III Quadrant, where sine is negative and cosine is negative.
we also know that angle B is in the II Quadrant, where sine is positive and cosine is negative.
the hypotenuse is never negative, since it's simply a radius length, so in a fraction, the hypotenuse will be the positive value.
![\bf sin(A)=\cfrac{\stackrel{opposite}{-8}}{\underset{hypotenuse}{17}}\qquad \impliedby \textit{let's find the \underline{adjacent side}} \\\\\\ \textit{using the pythagorean theorem} \\\\ c^2=a^2+b^2\implies \pm√(c^2-b^2)=a \qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(17^2-(-8)^2)=a\implies \pm√(225)=a\implies \pm 15 = a\implies \stackrel{III~Quadrant}{-15=a} \\\\\\ therefore\qquad \qquad cos(A)=\cfrac{-15}{17} \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2021/formulas/mathematics/high-school/67k2n8xj4ul0jmpootm9icakyju8nudjcf.png)
![\bf sec(B)=\cfrac{\stackrel{hypotenuse}{5}}{\underset{adjacent}{-4}}\qquad \impliedby \textit{let's find the \underline{opposite side}} \\\\\\ \pm√(c^2-a^2)=b\implies \pm√(5^2-(-4)^2)=b\implies \pm√(9)=b \\\\\\ \pm 3 = b\implies \stackrel{II~Quadrant}{3=b}~\hfill cos(B)=\cfrac{\stackrel{adjacent}{-4}}{\underset{hypotenuse}{5}}~\hfill sin(B)=\cfrac{\stackrel{opposite}{3}}{\underset{hypotenuse}{5}} \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2021/formulas/mathematics/high-school/chk3r4e3v8psoo4b4sd5569ppvp4qwfrgy.png)