Question

Segment AB was partitioned at a 1:3 ratio at point C. If point A is located at (3, 5) and point C is located at (6, 10). What are the coordinates of point B?

Question 2 options:

(12, 15)


(6, 10)


(9, 12)


(3, 1)

Question 3 (1 point)
Point G is located at (3, 2) and point H is located at (15, 8). What are the coordinates of the point that partitions the directed line segment GH in a 4:1 ratio?

Question 3 options:
Question 4 (1 point)
What are the coordinates of the midpoint of the line segment with endpoints B (9, -8) and C (2, -5).

Question 4 options:
Question 5 (1 point)
A directed line segment is a line that is divided into partitions.

Question 5 options:
True
False

Answer 1

Question 2:

We have that point C(6,10) partitions A(3,5) and B(a,b) in the ratio m:n=1:3

We use the section formula:

`(x,y)=((mx_2+nx_1)/(m+n), (my_2+ny_1)/(m+n))`

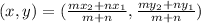
We substitute the values to get:

`(6,10)=((1*a+3*3)/(1+3), (1*b+3*5)/(1+3))`

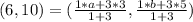
We simplify to get:

`(6,10)=((a+9)/(4), (b+15)/(4))`

This implies that:

`(6=(a+9)/(4),10= (b+15)/(4))`

`(24=a+9,40= b+15)`

`(a=15,b=25)`

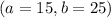
The coordinates of B are (15,25)

Question 3:

This time we have G(3,2) and H(15,8), and we want to find C(x,y) that partitions GH in a m;n=4:1 ratio:

We apply the section formula to get:

`(x,y)=((4*15+1*3)/(4+1), (4*8+1*2)/(4+1))`

`(x,y)=((60+3)/(5), (32+2)/(5))`

`(x,y)=((63)/(5), (34)/(5))`

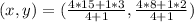
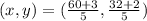
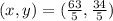
Question 4

We want to find the coordinates of the midpoint of the line segment with endpoints B (9, -8) and C (2, -5),

The midpoint is given by:

`(x,y)=((x_1+x_2)/(2), (y_1+y_2)/(2))`

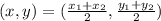
We substitute the endpoints to obtain:

`(x,y)=((9+2)/(2), (-1+-5)/(2))`

This simplifies to:

`(x,y)=((11)/(2), (-6)/(2))`

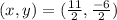
The midpoint is:

`(5(1)/(2), -3)`

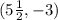
Question 5

A directed line segment has length and direction. That means there is a beginning point and an endpoint.

Partitions can occur on a directed line segments. This does not mean that all directed line segment must be partitioned.

Ans: False