Question

Which function has a greater rate of change over the interval [0,2]

9. Examine the graph of f(x) and the table that contains values of g(x). Which function has a greater rate of change over the interval [0,2]? Explain your answer.



x

-1
0
1
2
g(x)
7
5
7
13

Answer 1

g(x) has a greater average rate of change

Explanation:

From the given information, the table is:

x | g(x)

-1 7

0 5

1 7

2 13

From this table, we have g(0)=5 and g(2)=13

The average rate of change over [a,b] of g(x) is given by:
`(g(b)-g(a))/(b-a)`

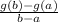
This implies that on the [0,2]. the average rate of change is:

`(g(2)-g(0))/(2-0)=(13-5)/(2)=(7)/(2)=3.5`

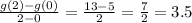
Also, we have that: f(0)=-4 and f(2)=-1.

This means that the average rate of change of f(x) on [0,2] is

`(f(2)-f(0))/(2-0)=(-1--4)/(2) =(3)/(2) =1.5`

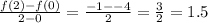
Hence g(x) has a greater average rate of change on [0,2]