Question

The length of a rectangle is 5cm more than it's width. If the width is increased by 2 cm and the length is increased by 3 cm a new rectangle is formed that has an area of 46 cm squared more than the original rectangle. Find dimensions of the original rectangle.

Answer 1

The dimensions of the original rectangle are:

Length 11 cm

Width 6 cm

Explanation:

Let

x ----> the original length

y ----> the original width

we know that

The original area is

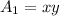`A_1=xy` ----> equation A

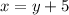`x=y+5` ----> equation B

The new area is

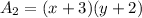`A_2=(x+3)(y+2)` ----> equation C

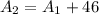`A_2=A_1+46` ----> equation D

substitute equation A and equation C in equation D

`(x+3)(y+2)=xy+46` ----> equation E

substitute equation B in equation E

`(y+5+3)(y+2)=(y+5)y+46`

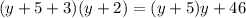
solve for y

(
`y+8)(y+2)=y^2+5y+46`

`y^2+10y+16=y^2+5y+46`

`10y-5y=46-16\\5y=30\\y=6\ cm`

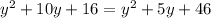
Find the value of x

`x=6+5=11\ cm`

therefore

The dimensions of the original rectangle are:

Length 11 cm

Width 6 cm