Question

How long would it take to double your money in an account paying 3​% compounded quarterly​?

Answer 1

It would take 23 years to double your money in an account paying 3​% compounded quarterly

Explanation:

Let the principal be 10

Then the Amount is 20

Time be n

Rate of interest = 3%

compounded quarterly be q =
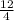`(12)/(4)` = 3

then

`n = (log(A/P))/((q log[1+(i/q)]))`

where i =
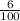`(6)/(100)` = 0.06

On substituting the values,

`n = (log((20)/(10)))/((3 * log[1+((0.03)/(3))]))`

`n = (0.3010)/(3 * log[1+ 0.01])`

`n = (0.3010)/(3 * log[1.01])`

`n = (0.3010)/(3 * 0.0043)`

`n = (0.3010)/(0.0129)`

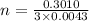
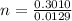
n = 23.333

n = 23