1 Answer

Ask a Question

Mkirk · Answer 1 · 2021-10-13T20:46:39+0000

Answer:

a) 101010 as a base 2 number is the same as 42 in base 10 and 2A in base 16

b) 42 as a base 10 number is same as 101010 in bases 2 and 2A in base 16

c) 2A as a base 16 number is same as 101010 in base 2 and 42 in base 10

Explanation:

a) When interpreting 101010 as a base 2 number, convert to bases 10 and 16;

First convert 101010 from base 2 to base 10

We number the digit from the rightmost digit starting from 0 and we have the following index:

1 = 5, 0 = 4, 1 = 3, 0 = 2, 1 = 1, 0 = 0

The we expand in the power of the index to base 2

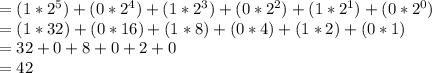
$= (1*2^(5)) + (0*2^(4)) + (1*2^(3)) + (0*2^(2)) + (1*2^(1)) + (0*2^(0))\\= (1 * 32) + (0 * 16) + (1 * 8) + (0 * 4) + (1 * 2) + (0 * 1)\\= 32 + 0 + 8 + 0 + 2 + 0\\= 42$

Then convert to base 16: divide base 10 by 16

42 ÷ 16 = 2 remainder 10(A)

2 ÷ 16 = 0 remainder 2

Reading the remainder bottom-up; we have 2A. 10 is represented as A in Base 16.

b) When interpreting 101010 as a base 10 number, convert to bases 2 and 16;

101010 in base 10 = 42

Converting to base 2

42 ÷ 2 = 21 remainder 0

21 ÷ 2 = 10 remainder 1

10 ÷ 2 = 5 remainder 0

5 ÷ 2 = 2 remainder 1

2 ÷ 2 = 1 remainder 0

1 ÷ 2 = 0 remainder 1

Reading the remainder bottom-up; we have 101010 in base 2

Then convert to base 16: divide base 10 by 16

42 ÷ 16 = 2 remainder 10(A)

2 ÷ 16 = 0 remainder 2

Reading the remainder bottom-up; we have 2A. 10 is represented as A in Base 16.

c) When interpreting 101010 as a base 16 number, convert to bases 2 and 10

Converting from base 16 to base 10; we expand in the power of the index:

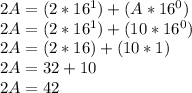
$2A = (2 * 16^(1) ) + (A * 16^(0))\\2A = (2 * 16^(1) ) + (10 * 16^(0))\\2A = (2 * 16 ) + (10 * 1)\\2A = 32 + 10\\2A = 42$