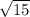Question

Given the planes P1 : x + 4y − z = 10, P2 : 3x − y + 2z = 4, and the point A (−2, 1, 0).

(a) Determine an equation for the plane that contains A and is parallel to P1.
(b) Determine whether A lies on P2. If it doesn’t, find the distance from A to P2.

Answer 1

a) x+4y-z=2

b) -7/
`√(15)`

Explanation:

a)

Equation of a plane containing point A is given by;

[x-(-2)]+[y-1]+[z-0]=0 ----(1)

If this plane is parallel to the plane P1 whose normal vector is {1.4.-1] - then this will also be normal to plane (1)

so,

(1)[x-(-2)]+(4)[y-1]+(-1)[z-0]=0

==> x+2+4y-4-z=0

==> x+4y-z=2

will be the plane parallel to P1
`√(15)`

b) If A lies on P2 then it should satisfy the equation of P2

Putting x= -2, y=1 and z= 0

==> 3(-2)-(1)+2(0)=4

==>-6-1+0=4

==> 5=4

which is not true i-e equation is not satisfied ! So the point lies out of plane. Lets find distance from P2 of point A

We know distance of point (x1,y1,z1) from a plane Ax+By+CZ+D=0 is

d= Ax1+By1+Cz1+D /
`\sqrt{A^(2)+B^(2)+C^(2) }`

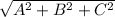
So distance of point A from P2 is;

d= 3×(-2)-1(1)+2(0)/
`√(9+1+4)`

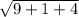
==> d= -7/
`√(15)`