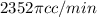The volume of the balloon is
Step-by-step explanation:
The radius of the balloon is increasing at a rate of 3 cm/min.
To determine the volume of the balloon when the radius is 14 cm, we shall use the formula
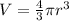
The rate of change of r with respect to time t is given by,
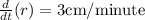
Now, we shall determine the
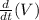
Now, we shall determine the
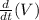 at
at
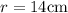 and substituting
and substituting
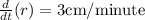 , we get,
, we get,

Thus, The volume of the balloon is