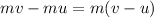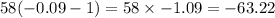Answer:
a. 0.91 m/s
b. -63.22 kg.m/s
Step-by-step explanation:
The principle of conservation of momentum states that the total momentum before collision is equal to the total momentum after collision in an isolated system.
If we assume the collision is isolated, then the total initial momentum is the sum of the momentum of the girl and that of the partner. Since the partner was at rest, his initial momentum is 0.
After collision, both glided with the same velocity which is in the direction of the girl's initial velocity.
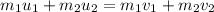
Quantities with subscript 1 are for the girl and those with 2 are for the partner.
 represents mass,
represents mass,
 represents initial velocity and
represents initial velocity and
 represents final velocity. Since the final velocities are the same,
represents final velocity. Since the final velocities are the same,
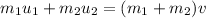
where
 is the common velocity
is the common velocity
Substitute known quantities.
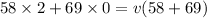
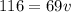
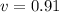
b. With respect to the skater, the girl's initial velocity =
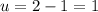
And the final velocity =
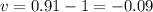
Change in momentum =