Answer:
Option a : 26.26 to 35.74 .
Explanation:
We are provided a random sample of 15 employees of which average age in the sample, xbar = 31 years and Standard Deviation, s =
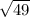 = 7 years.
= 7 years.
We know that
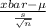 follows
follows

So, 98% confidence interval is given by ;
P(-2.624 <
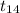 < 2.624) = 0.98 {because at 14 degree of freedom t table
< 2.624) = 0.98 {because at 14 degree of freedom t table
gives critical value of 2.624 at 1% level}
P(-2.624 <
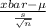 < 2.624) = 0.98
< 2.624) = 0.98
P(-2.624*
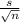 <
<
 < 2.624*
< 2.624*
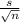 ) = 0.98
) = 0.98
P(xbar - 2.624*
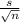 <
<
 < xbar + 2.624*
< xbar + 2.624*
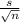 ) = 0.98
) = 0.98
98% Confidence Interval for
 = [xbar - 2.624*
= [xbar - 2.624*
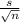 , xbar + 2.624*
, xbar + 2.624*
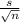 ]
]
= [
 ,
,
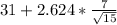 ]
]
= [26.26 , 35.74]
Therefore, 98% confidence interval for the population average age is 26.26 to 35.74 .