Question

The mean number of hours per day spent on the phone, according to a national survey, is four hours, with a standard deviation of two hours. If each time was increased by one hour, what would be the new mean and standard deviation? (2 points)

Select one:
a. 4, 2
b. 4, 3
c. 5, 2
d. 5, 3

Answer 1

The new mean is 5.

The new standard deviation is also 2.

Explanation:

Let the sample space of hours be as follows, S = {x₁, x₂, x₃...xₙ}

The mean of this sample is 4. That is,
`\bar x=(x_(1)+x_(2)+x_(3)+...+x_(n))/(n)=4`

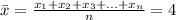
The standard deviation of this sample is 2. That is,
`s=(1)/(n-1)\sum (x_(i)-\bar x)^(2)=2`.

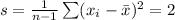Now it is stated that each of the sample values was increased by 1 hour.

The new sample is: S = {x₁ + 1, x₂ + 1, x₃ + 1...xₙ + 1}

Compute the mean of this sample as follows:

`\bar x_(N)=(x_(1)+1+x_(2)+1+x_(3)+1+...+x_(n)+1)/(n)\\=((x_(1)+x_(2)+x_(3)+...+x_(n)))/(n)+((1+1+1+...n\ times))/(n)\\=\bar x+1\\=4+1\\=5`

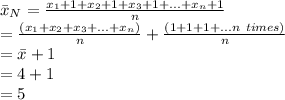
The new mean is 5.

Compute the standard deviation of this sample as follows:

`s_(N)=(1)/(n-1)\sum (x_(i)-\bar x)^(2)\\=(1)/(n-1)\sum ((x_(i)+1)-(\bar x+1))^(2)\\=(1)/(n-1)\sum (x_(i)+1-\bar x-1)^(2)\\=(1)/(n-1)\sum (x_(i)-\bar x)^(2)\\=s`

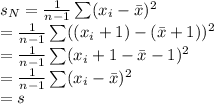
The new standard deviation is also 2.