The question is incomplete, here is the complete question:
A chemist titrates 110.0 mL of a 0.2412 M hypochlorous acid (HCIO) solution with 0.0613 M NaOH solution at 25°C. Calculate the pH at equivalence. The pKa of hypochlorous acid is 7.50. Round your answer to 2 decimal places
Answer: The pH of the solution is 10.09
Step-by-step explanation:
To calculate the volume of base, we use the equation given by neutralization reaction:

where,
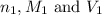 are the n-factor, molarity and volume of acid which is
are the n-factor, molarity and volume of acid which is
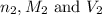 are the n-factor, molarity and volume of base which is NaOH.
are the n-factor, molarity and volume of base which is NaOH.
We are given:
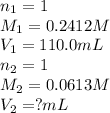
Putting values in above equation, we get:
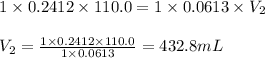
At equivalence, the number of moles of acid is equal to the number of moles of base. Also, the moles of salt which is NaClO will also be the same.
To calculate the number of moles for given molarity, we use the equation:
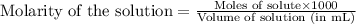 .....(1)
.....(1)
Molarity of HClO solution = 0.2412 M
Volume of solution = 110.0 mL
Putting values in equation 1, we get:
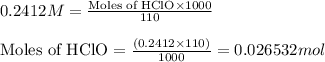
Moles of NaClO = 0.026532 moles
Volume of solution = [432.8 + 110] mL = 542.8 mL
Putting values in above equation, we get:
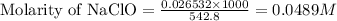
To calculate the pH of the solution, we use the equation:
![pH=7+(1)/(2)[pK_a+\log C]](https://img.qammunity.org/2021/formulas/chemistry/college/1ksvvke1tt2nowop1riavu47gnezphkoxo.png)
where,
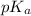 = negative logarithm of weak acid which is hypochlorous acid = 7.50
= negative logarithm of weak acid which is hypochlorous acid = 7.50
C = concentration of the salt = 0.0489 M
Putting values in above equation, we get:
![pH=7+(1)/(2)[7.50+\log (0.0489)]\\\\pH=7+3.09=10.09](https://img.qammunity.org/2021/formulas/chemistry/college/ub5bkb0gcf433fepe0vb7t4rwwr2pqc80c.png)
Hence, the pH of the solution is 10.09