Question:
When circuit boards used in the manufacture of compact disc players are tested, the long-run percentage of defectives is 5%. Let x denote the number of defective boards in a batch of 25 boards, so that x has a binomial distribution with n = 25 and π = 0.05.
(a) What proportion of batches have at most 2 defective boards?
(b) What proportion of batches have at least 5 defective boards?
(c) What proportion of batches will have all 25 boards free of defects?
Answer:
(a) Proportion of batches have at most 2 defective boards 0.87291.
(b) Proportion of batches have at least 5 defective boards is 0.00714.
(c) Proportion of batches will have all 25 boards free of defects is 0.2774.
Solution:
n= 25, π = 0.05
Binomial distribution formula:

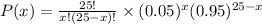
(a) Proportion with x = 0 is given by
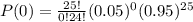
P(0) = 0.2774
Proportion with x = 1 is given by

P(1) = 0.36499
Proportion with x = 2 is given by

P(2) = 0.23052
Proportion with at most 2 defective = P(x ≤ 2)
= P(0) + P(1) + P(2)
= 0.2774 + 0.36499 + 0.23052
Proportion with at most 2 defective = 0.87291
(b) Proportion with x = 3 is given by
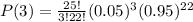
P(3) = 0.093
Proportion with x = 4 is given by
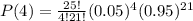
P(4) = 0.2693
Proportion with x ≥ 5 = 1 – P(x ≤ 5)
= 1 – (P(0) + P(1) + P(2) + P(3) + P(4))
= 1 – (0.2774 + 0.36499 + 0.23052 + 0.093 + 0.093)
= 0.00714
Proportion of batches have at least 5 defective boards is 0.00714.
(c) Proportion with x = 0
It is already found in (a).
Proportion of batches will have all 25 boards free of defects is 0.2774.