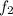Question

The air in a pipe resonates at 150 Hz and 750 Hz, one of these resonances being the fundamental. If the pipe is open at both ends, how many resonances are between the two given ones, and if the pipe is closed at one end, how many resonances are between the two given ones?

Answer 1

Step-by-step explanation:

Two frequencies with magnitude 150 Hz and 750 Hz are given

For Pipe open at both sides

fundamental frequency is 150 Hz as it is smaller

frequency of pipe is given by

`f=(nv)/(2L)`

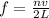
where L=length of Pipe

v=velocity of sound

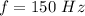`f=150\ Hz` for n=1

and f=750 is for n=5

thus there are three resonance frequencies for n=2,3 and 4

For Pipe closed at one end

frequency is given by

`f=((2n+1))/(4L)\cdot v`

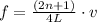
for n=0

`f_1=(v)/(4L)`

`f_1=150\ Hz`

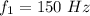
for n=2

`f_2=(5v)/(4L)`

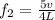
Thus there is one additional resonance corresponding to n=1 , between
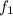`f_1` and
`f_2`