Question

How do you do this question?

Answer 1

20

Explanation:

A left Riemann sum approximates a definite integral as:

`\int\limits^b_a {f(x)} \, dx \approx \sum\limits_(k=1)^(n)f(x_(k)) \Delta x \\where\ \Delta x = (b-a)/(n) \ and\ x_(k)=a+\Delta x * (k-1)`

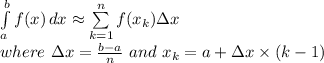
Here, the integral is ∫₀² 9ˣ dx, and the number of subintervals is n = 4.

So Δx = 2/n = 1/2, and x = 2(k−1)/n = (k−1)/2.

Plugging in:

∑₁⁴ 9^((k−1)/2) (1/2)

1/2 ∑₁⁴ 9^((k−1)/2)

1/2 (9^((1−1)/2) + 9^((2−1)/2) + 9^((3−1)/2) + 9^((4−1)/2))

1/2 (9^(0) + 9^(1/2) + 9^(1) + 9^(3/2))

1/2 (1 + 3 + 9 + 27)

20