Part A:
In triangle ABC and DEF,
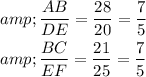
If the ratios of lengths of the sides of two triangles are same, then the triangles are similar.
Therefore ΔABC
 ΔDEF.
ΔDEF.
Scale factor of two triangles =
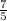
Part B:
Suppose height of the prism made by ΔABC = 15 inches
Volume of the prism made by ΔABC = Area of the triangle × height

= 4410 inch³
Volume of the prism made by ΔABC = 4410 inch³
Part C: Suppose the volume of the prism made by ΔABC = 4459 inch³
Volume of the larger prism = (Scale factor)² × volume of the smaller triangle
Volume of the larger prism =
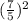 × volume of the smaller triangle
× volume of the smaller triangle
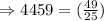 × volume of the smaller triangle
× volume of the smaller triangle
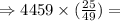 volume of the smaller triangle
volume of the smaller triangle
Volume of the smaller triangle ΔDEF = 2275 inch³