Question

A ball is projected horizontally from the top of a building. One second later, another ball is projected horizontally from the same point with the same velocity. At what point in the motion will the balls be closest to each other

Answer 1

t = 0 at the start of the projection

Explanation:

To solve this we need to find the distance between the 2 positions at any given time, then solve for the least distance

Let t be the time of the 2nd ball, so t + 1 is the time of the first ball

Let g be the gravitational acceleration, v be the horizontal velocity

the y coordinates of the first and 2nd balls

`y_1 = -g(t+1)^2/2`

`y_2 = -gt^2/2`

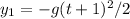
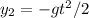
The x coordinates of the 1st and 2nd balls:

`x_1 = v(t+1)`

`x_2 = vt`

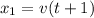
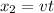
The distance between the 2 balls is

`d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

`d = √((v(t + 1) - vt)^2 + (-g(t+1)^2/2 - (-gt^2/2))^2)`

`d = √((vt + v - vt)^2 + g/4(t^2 - (t^2 + 2t + 1))^2)`

`d = √(v^2 + (g/4)(-2t-1)^2)`

`d = √(v^2 + (g/4)(2t+1)^2)`

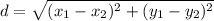
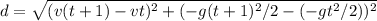
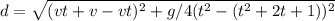
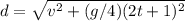
As both v and g are constant and cannot be changed, d is minimum when (2t + 1) is minimum, which happens only when t is minimum = 0