Question

According to the University of Nevada Center for Logistics Management, 6% of all mer-

chandise sold in the United States gets returned (BusinessWeek, January 1 5, 2007). A
Houston department store sampled 80 items sold in January and found that 12 of the items
were returned.
a. Construct a point estimate of the proportion of items returned for the population of
sales transactions at the Houston store.
b. Construct a 95% confidence interval for the porportion of returns at the Houston store.
c. Is the proportion of returns at the Houston store significantly different from the returns
for the nation as a whole? Provide statistical support for your answer.

Answer 1

a) The point estimate of the proportion of items returned for the population of

sales transactions at the Houston store = 12/80 = 0.15

b) The 95% confidence interval for the proportion of returns at the Houston store = [0.0718 < p < 0.2282].

c) Yes.

We set an hypothesis and construct a test statistics. The test statistics result gives us:

Z calculated = 2.2545, and this gives us the p-value = 0.0121. We assumed 95% confident interval. Hence, the level of significance (α) = 5%. Conclusively, since the p-value ==> 0.0121 is less than (α) = 5%, the test is significant. Hence, the proportion of returns at the Houston store is significantly different from the returns for the nation as a whole.

Explanation:

a) Point estimate of the proportion = number of returned items/ total items sold = 12/80 = 0.15.

b) By formula of confident interval:

CI(95%) = p ± Z*
`\sqrt{(p*(1-p))/(n) } = 0.15 \pm 1.96 *\sqrt{(0.15*(1-0.15))/(80) }`,

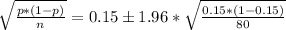CI(95%) = [0.0718 < p < 0.2282]

c) The hypothesis:

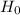`H_(0)`: The proportion of returns at the Houston store is not significantly different from the returns for the nation as a whole.

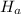`H_(a)`: The proportion of returns at the Houston store is significantly different from the returns for the nation as a whole.

The test statistics:

Z =
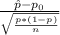`\frac{\hat{p} - p_(0)}{\sqrt{(p*(1-p))/(n) }}`, where
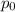`p_(0)` is the proportion of nation returns.

Z calculated = 2.2545, and this gives us the p-value = 0.0121. We assumed 95% confident interval. Hence, the level of significance (α) = 5%. Conclusively, since the p-value ==> 0.0121 is less than (α) = 5%, the test is significant. Hence, the proportion of returns at the Houston store is significantly different from the returns for the nation as a whole.