Question

The rule r y-axis R 0,90^ (x,y) is applied to triangle ABC . Which triangle shows the final image?

ANSWER: A) 1

Answer 1

Answer: 1

Explanation:

Answer 2

1

Explanation:

Given triangle ABC with vertices at points A(2,-4), B(4,-4) and C(4,-2).

1. Rotate this triangle anticlockwise by 90° angle over the origin. This rotation has the rule

`(x,y)\rightarrow (-y,x),`

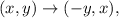
then

`A(2,-4)\rightarrow A'(4,2)\\ \\B(4,-4)\rightarrow B'(4,4)\\ \\C(4,-2)\rightarrow C'(2,4)`

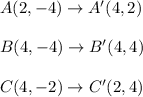
2. Reflect triangle A'B'C' across the y-axis. This reflection has the rule

`(x,y)\rightarrow (-x,y),`

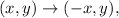
then

`A'(4,2)\rightarrow A''(-4,2)\\ \\B'(4,4)\rightarrow B''(-4,4)\\ \\C'(2,4)\rightarrow C''(-2,4)`

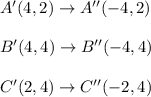
These are vertices of triangle 1