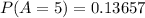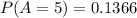Answer:
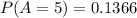
Explanation:
From each multiple-choice question, there consists three answers to each;
So the probability of picking, the correct answer as they are uniformly distributed among the choices (a), (b), and (c) will be;
P(correct answer) =

Now, to determine the probability of obtaining exactly 5 correct answers on a ten question examination using this method
Let use A as representative for the numbers of correct answers out of 10 questions that is being answered.
∴
![P(A=5)= [\left \ {{10} \atop {5}} \right.]](https://img.qammunity.org/2021/formulas/mathematics/college/lcgwgsdmqiok6g67oy6w82a0at6qeodx5m.png)
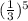

/(3)) ^5 ((2)/(3)) ^5](https://img.qammunity.org/2021/formulas/mathematics/college/cyvdbhfv0lfbva2sl1gkwl638bg3mv8zid.png)