Question

A rival pirate fires his volley back at the same 3.5m above the sea but at an angle of 23 coincidentally this scurvy dogs cannon also fires at 120 m/s also strangely coincidentally this cannonball also misses the sea how far did this canon ball travel?

Answer 1

1.065 km

Step-by-step explanation:

The horizontal and vertical component of the canon ball when it's fired is

`v_h = vcos\alpha = 120cos23^0 = 110.46 m/s`

`v_v = vsin\alpha = 120sin23^0 = 46.89 m/s`

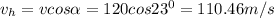
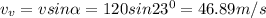
If we ignore air resistance, then gravitational acceleration g = -9.8m/s2 is the only thing that affects the vertical motion of the cannon ball. We can use the following equation to calculate the time it stays on air after it traveling h = -3.5m (down below the firing point) vertically

`h = v_vt + gt^2/2`

`-3.5 = 46.89t - 9.8t^2/2`

`-4.9t^2 + 46.89t + 3.5 = 0`

`t= (-b \pm √(b^2 - 4ac))/(2a)`

`t= (-46.89\pm √((46.89)^2 - 4*(-4.9)*(3.5)))/(2*(-4.9))`

`t= (-46.89\pm47.62)/(-9.8)`

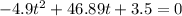
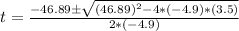
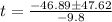
t = -0.07 or t = 9.64

Since t can only be positive we will pick t = 9.64

This is also the time it takes for the cannon ball to travel horizontally at the rate of 110.46 m/s

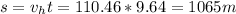`s = v_ht = 110.46 * 9.64 = 1065 m` or 1.065 km