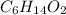Question

A solution contains 10.20 g of unknown compound (non-electrolyte) dissolved in 50.0 mL of water. (Assume a density of 1.00 g/mL for water.) The freezing point of the solution is -3.21 ∘C. The mass percent composition of the compound is 60.98% C, 11.94% H, and the rest is ?

Answer 1

The question is incomplete, here is the complete question:

A solution contains 10.20 g of unknown compound dissolved in 50.0 mL of water. (Assume a density of 1.00 g/mL for water.) The freezing point of the solution is -3.21°C. The mass percent composition of the compound is 60.98% C , 11.94% H , and the rest is O.

What is the molecular formula of the compound?

Answer: The molecular formula for the given organic compound is
`C_6H_(14)O_2`

Step-by-step explanation:

• To calculate the mass of water, we use the equation:

`\text{Density of substance}=\frac{\text{Mass of substance}}{\text{Volume of substance}}`

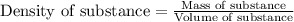
Density of water = 1 g/mL

Volume of water = 50.0 mL

Putting values in above equation, we get:

`1g/mL=\frac{\text{Mass of water}}{50.0mL}\\\\\text{Mass of water}=(1g/mL* 50.0mL)=50g`

Depression in freezing point is defined as the difference in the freezing point of pure solution and the freezing point of solution

The equation used to calculate depression in freezing point follows:

`\Delta T_f=\text{Freezing point of pure solution}-\text{freezing point of solution}`

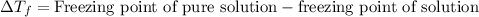
• To calculate the depression in freezing point, we use the equation:

`\Delta T_f=i* K_f* m`

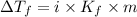
Or,

`\text{Freezing point of pure solution}-\text{freezing point of solution}=i* K_f* \frac{m_(solute)* 1000}{M_(solute)* W_(solvent)\text{ (in grams)}}`

where,

Freezing point of pure solution (water) = 0°C

Freezing point of solution = -3.21°C

i = Vant hoff factor = 1 (For non-electrolytes)

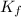`K_f` = molal boiling point elevation constant = 1.86°C/m

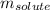`m_(solute)` = Given mass of solute = 10.20 g

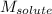`M_(solute)` = Molar mass of solute = ?

`W_(solvent)` = Mass of solvent (water) = 50.0 g

Putting values in above equation, we get:

`(0-(-3.21))^oC=1* 1.86^oC/m* (10.20* 1000)/(M_(solute)* 50)\\\\M_(solute)=(1* 1.86* 10.20* 1000)/(3.21* 50)=118.2g`

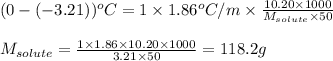
Calculating the molecular formula:

We are given:

Percentage of C = 60.98 %

Percentage of H = 11.94 %

Percentage of O = (100 - 60.98 - 11.94) % = 27.08 %

Let the mass of compound be 100 g. So, percentages given are taken as mass.

Mass of C = 60.98 g

Mass of H = 11.94 g

Mass of O = 27.08 g

To formulate the empirical formula, we need to follow some steps:

• Step 1: Converting the given masses into moles.

Moles of Carbon =
`\frac{\text{Given mass of Carbon}}{\text{Molar mass of Carbon}}=(60.98g)/(12g/mole)=5.082moles`

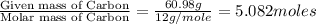
Moles of Hydrogen =
`\frac{\text{Given mass of Hydrogen}}{\text{Molar mass of Hydrogen}}=(11.94g)/(1g/mole)=11.94moles`

Moles of Oxygen =
`\frac{\text{Given mass of oxygen}}{\text{Molar mass of oxygen}}=(27.08g)/(16g/mole)=1.69moles`

• Step 2: Calculating the mole ratio of the given elements.

For the mole ratio, we divide each value of the moles by the smallest number of moles calculated which is 1.69 moles.

For Carbon =
`(5.082)/(1.69)=3`

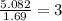
For Hydrogen =
`(11.94)/(1.69)=7.06\approx 7`

For Oxygen =
`(1.69)/(1.69)=1`

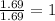
• Step 3: Taking the mole ratio as their subscripts.

The ratio of C : H : O = 3 : 7 : 1

The empirical formula for the given compound is
`C_3H_7O`

For determining the molecular formula, we need to determine the valency which is multiplied by each element to get the molecular formula.

The equation used to calculate the valency is:

`n=\frac{\text{Molecular mass}}{\text{Empirical mass}}`

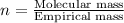
We are given:

Mass of molecular formula = 118.2 g/mol

Mass of empirical formula = 59 g/mol

Putting values in above equation, we get:

`n=(118.2g/mol)/(59g/mol)=2`

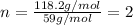
Multiplying this valency by the subscript of every element of empirical formula, we get:

`C_((3* 2))H_((7* 2))O_((1* 2))=C_6H_(14)O_2`

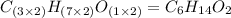
Hence, the molecular formula for the given organic compound is
`C_6H_(14)O_2`