Question

Two equipotential surfaces surround a +1.38 10-8-C point charge. How far is the 179-V surface from the 67.5-V surface?

Answer 1

The question is incomplete, below is the complete question

"Two equipotential surfaces surround a +1.38*10^-8C point charge. How far is the 179-V surface from the 67.5-V surface? "

Answer:

1.15m

Step-by-step explanation:

From the formula connecting the charge, potential and the distance i.e

`V=(kq)/(r)`

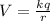
where q=charge, k=constant and r=distance between the points

the data given in the question are

`q=1.38*10^(-8)c,\\V_(1)=179v\\V_(2)=67.5v\\r_(1)-r_(2)=??`

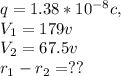
We can express the distance from the charge to the equipotential surface as

`r_(1)=(kq)/(v_(1))\\`

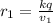
for the second charge we have

`r_(2)=(kq)/(v_(2))\\`

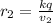
The distance between the two surface is

`r_(2)-r_(1)=(kq)/(v_(2))-(kq)/(v_(1))\\r_(2)-r_(1)=kq((1)/(v_(2))-(1)/(v_(1)))\\r_(2)-r_(1)=(9*10^(9)*1.38*10^(-8))((1)/(67.5)-(1)/(179))\\r_(2)-r_(1)=124.2(0.0148-0.00558)\\r_(2)-r_(1)=1.15m`

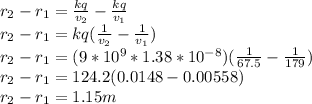
Hence the distance is 1.15m