Question

Carrie and Ryan have both computed the slope of the least-squares line using data for which the standard deviation of the x-values and the standard deviation of the y-values are equal. Carrie gets a value of 0.5 for the slope, and Ryan gets a value of 2. One of them is right. Which one?

Answer 1

Carrie's slope value is correct.

Explanation:

The least square regression line is:
`(y -\bar y)=b_(yx) (x-\bar x)`

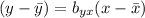
Here
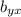`b_(yx)` is the slope of the line.

The formula to compute the slope is:

`b_(yx)=r(\sigma_(x))/(\sigma_(y))`

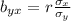
Here
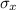`\sigma_(x)` = standard deviation of x and
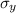`\sigma_(y)` = standard deviation of y.

It is provided that the standard deviation of x and y are equal.

So the slope of the regression line is:

`b_(yx)=r(\sigma_(x))/(\sigma_(y))=r(\sigma_(x))/(\sigma_(x))=r`

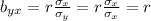
Thus, if the standard deviation of x and y are equal the slope of the line is same as the correlation coefficient.

The correlation coefficient is a measure used to determine the strength of the linear relationship between the variables.

It ranges from -1 to 1.

Carrie's slope value was 0.50 and Ryan's slope value was 2.

Since -1 ≤ r ≤ 1 the value of slope cannot be 2.

Thus, Ryan's slope value is incorrect.