Question

Two containers, X and Y, are each filled by an ideal gas at the same temperature. The volume of Y is half the volume of X. The number of moles of gas in Y is three times the number of moles of the gas in X. The pressure of the gas in X is PX and the pressure of the gas in Y is PY. What is the ratio LaTeX: \frac{P_X}{P_Y}P Y P Y

Answer 1

The answer to the question is

The ratio of the two gas pressures
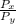`(P_(x) )/(P_(y) )` , that is Px to Py = 1/6

Explanation:

Let the gases Volumes be V₁ and V₂

Where volume of X = V₁ and

volume of Y = V₂

The volume of Y is half the volume of X

∴ V₂ =
`(1)/(2)` × V₁

Let the number of moles be n₁ and n₂ in X and Y respectively

therefore n₂ = 3 × n₁

The pressure of the gas in X is Pₓ and the pressure of the gas in Y is
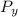`P_(y)` then we have

P₁ × V₁ = n₁ × R × T₁ , and P₂ × V₂ = n₂ × R × T₂

(P₁ × V₁)/(n₁ × T₁) = (P₂ × V₂)/(n₂ × T₂)

but T₁ = T₂

Therefore

(P₁ × V₁)/n₁ = (P₂ × V₂)/n₂. However n₂ = 3 × n₁ and V₂ =
`(1)/(2)` × V₁ therefore substituting in the equation we have

(P₁ × V₁)/n₁ = (P₂ ×
`(1)/(2)` × V₁ )/(3 × n₁) from where

P₁ /P₂ = (
`(1)/(2)` × V₁ × n₁)/(V₁×3 × n₁) =0.5/3 = 1/6

The ratio of
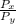`(P_(x) )/(P_(y) )` = 1/6