Question

Consider the relationship below, given StartFraction pi Over 2 EndFraction less-than theta less-than pi. sine squared theta + cosine squared theta = 1 Which of the following best explains how this relationship and the value of sin Theta can be used to find the other trigonometric values? The values of sin Theta and cos Theta represent the legs of a right triangle with a hypotenuse of 1; therefore, solving for cos Theta finds the unknown leg, and then all other trigonometric values can be found. The values of sin Theta and cos Theta represent the angles of a right triangle; therefore, solving the relationship will find all three angles of the triangle, and then all trigonometric values can be found. The values of sin Theta and cos Theta represent the angles of a right triangle; therefore, other pairs of trigonometric ratios will have the same sum, 1, which can then be used to find all other values. The values of sin Theta and cos Theta represent the legs of a right triangle with a hypotenuse of –1, since Theta is in Quadrant II; therefore, solving for cos Theta finds the unknown leg, and then all other trigonometric values can be found.

Answer 1

A

Step-by-step explanation:

just took the test

Answer 2

• First option: The values of sinθ and cosθ represent the legs of a right triangle with a hypotenuse of 1; therefore, solving for cosθ finds the unknown leg, and then all other trigonometric values can be found.

Step-by-step explanation:

1. Given:

`\pi /2<\theta <\pi\\ \\ sin^2\theta +cos^2\theta =1`

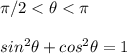
2. Known:

It is stated that the value of
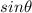`sin\theta` is known and you want to know how this value and the relationship can be used to find the other trigonometric values.

2. Solution:

a) Quadrant

The quadrants are:

`0<\theta<\pi /2:first\text{ }quadrant \\ \\\pi /2<\theta <\pi:second\text{ }quadrant\\ \\ \pi<\theta<3\pi/2:third\text{ }quadrant\\ \\ 3\pi/2<\theta<2\pi:fourth\text{ }quadrant`

Hence the angle is in the second quadrant.

In the second quadrant the x-coodinate is negative and the y-coordinate is positive.

In the unit circle, the x-coordinate is the cosine value, and the y-coordinate is the sine valu.

Then, when you draw a right triangle using a point on the unit circle, the cosine is the horizontal leg, the sine is the vertical leg, and the hypotenuse is 1.

Hence, when you know the sine of the angle, you know the horizontal leg of the right triangle, and using the relation
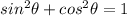`sin^2\theta +cos^2\theta =1` you can solve for the other trigonometric function, cosine.

`cos\theta =\pm √(1-sin^2\theta)`

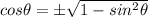
From that relation the cosine function can have two values.

You choose the negative value, because you are in the second quadrant, where the x-coordinate is negative.

Also, once you have the cosine function, you will be able to calculate the tangent, because:

`tan\theta =sin\theta /cos\theta`

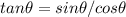
The other trigonometric functions are cosecant, secant, and cotangent, which are just the inverse of sine, cosine, and tangent, respectively.

Therefore, it is demonstrated the first statement.