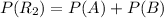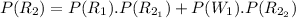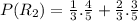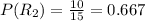Question

Suppose you have two urns with poker chips in them. Urn I contains two red chips and four white chips.Urn II contains three red chips and one white chip. You randomly select one chip from urn I and put itinto urn II. Then you randomly select a chip from urn II.What is the probability that the chip you select from urn II is red?

Answer 1

`P(R_(2)) =(10)/(15) = 0.667`

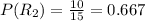
Explanation:

Step 1: Understanding the possible events

Selecting a chip from Urn I and then adding that chip to Urn II and then selecting a red chip from Urn II can be completed in two ways:

A. Selecting a red chip from Urn I and adding it to Urn II and then selecting a red chip from Urn II

B. Selecting a white chip from Urn I and adding it to Urn II and then selecting a red chip from Urn II

Therefore total probability is:

`P(R_(2)) = P(A) + P(B)`

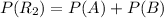
Step 2: Probability of selecting either chip from Urn I

Urn I contains 2 reds and 4 white chips, that gives a total of 6 chips.

`P(R_(1)) = (2)/(6) =(1)/(3)`

`P(W_(1)) = (4)/(6) =(2)/(3)`

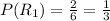
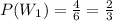
Step 3: Probability of selecting a red chip from Urn II

Urn II originally contains 3 reds and 1 white chip, that gives a total of 4 chips.

Remember: Once a chip is added from Urn I to Urn II the total number of chips will increase in the Urn II

Case 1: When a red chip is added from Urn I to Urn II

Red chips = 4

White chips = 1

Total Chips = 5

`P(R_(2_1)) = (4)/(5)`

Case 2: When a white chip is added from Urn I to Urn II

Red chips = 3

White chips = 2

Total Chips = 5

`P(R_(2_2)) = (3)/(5)`

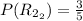
Therefore the total Probability of selecting a chip from Urn I and then adding that chip to Urn II and then selecting a red chip from Urn II can be calculated as:

`P(R_(2)) = P(A) + P(B)`

`P(R_(2)) = P(R_(1)) . P(R_(2_1)) + P(W_(1)) . P(R_(2_2))`

`P(R_(2)) =(1)/(3) . (4)/(5) + (2)/(3) .(3)/(5)`

`P(R_(2)) =(4)/(15) + (2)/(5)`

`P(R_(2)) =(10)/(15) = 0.667`