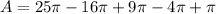Question

The five circles making up this archery target have diameters of length $2,4,6,8,$ and $10$. What is the total red area?

Simplify your answer as much as you can. You can use pi in your answer if necessary (for example, if the answer were $3\pi$, you could enter "3pi" or "3*pi" or "$3\pi$").

[asy]

size(4cm);

path a=Circle((0,0),5);

path b=Circle((0,0),4);

path c=Circle((0,0),3);

path d=Circle((0,0),2);

path e=Circle((0,0),1);

fill(a,red); fill(b,white); fill(c,red); fill(d,white); fill(e,red);

[/asy]
This is from Artofproblemsolving.com and yes my age here is not my real age i just chose a random year

Answer 1

`A=15\pi\ units^2`

Explanation:

The picture of the question in the attached figure

we know that

It is given that the diameter of 5 circles making up the archery is 2,4,6,8, and 10.

To determine the total red area, we use the formula for area of the circle

`A=\pi r^(2)`

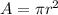
step 1

Find the Area of the 1st red circle

`r=2/2=1\ unit` ---> the radius is half the diameter

`A_1=\pi (1)^(2)=\pi\ units^2`

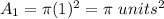
step 2

Find the Area of the 2nd white circle

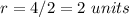`r=4/2=2\ units` ---> the radius is half the diameter

`A_2=\pi (2)^(2)=4\pi\ units^2`

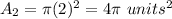
step 3

Find the Area of the 3rd red circle

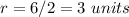`r=6/2=3\ units` ---> the radius is half the diameter

`A_3=\pi (3)^(2)=9\pi\ units^2`

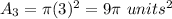
step 4

Find the Area of the 4th white circle

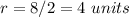`r=8/2=4\ units` ---> the radius is half the diameter

`A_4=\pi (4)^(2)=16\pi\ units^2`

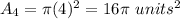
step 5

Find the Area of the 5th red circle

`r=10/2=5\ units` ---> the radius is half the diameter

`A_5=\pi (5)^(2)=25\pi\ units^2`

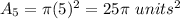
The total red area is given by

`A=A_5-A_4+A_3-A_2+A_1`

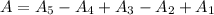
substitute

`A=25\pi-16\pi+9\pi-4\pi+\pi`

`A=15\pi\ units^2`