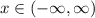Answer:
a)
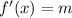
b)
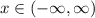
c)
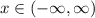
Explanation:
We are given the following in the question:
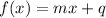
a) We have to find the derivative of the given function.
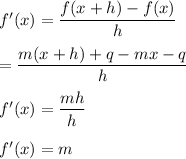
b) Domain of f(x)
Domain is the collection of all values of x for which the function is defined.
Domain of f(x) is all real numbers.
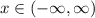
c) Domain of f'(x)
Domain of f'(x) is all real numbers.