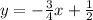Answer:
Part A)
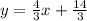
Part B)
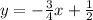
Explanation:
Part A) Passes through (−2, 2) and parallel to 4x − 3y − 7 = 0
we have
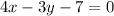
Isolate he variable y
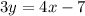
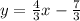
The slope of the given line is
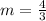
Remember that
If two lines are parallel then their slopes are the same
therefore
The slope of the line parallel to the given line is also
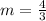
Find the equation of the line in slope intercept form
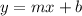
we have
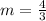
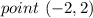
substitute
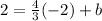
solve for b
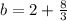
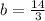
therefore
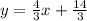
Part B) Passes through (−2, 2) and perpendicular to 4x − 3y − 7 = 0
we have
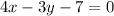
Isolate he variable y
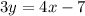
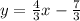
The slope of the given line is
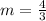
Remember that
If two lines are perpendicular, then their slopes are opposite reciprocal
therefore
The slope of the line perpendicular to the given line is
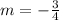
Find the equation of the line in slope intercept form
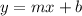
we have
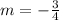
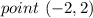
substitute
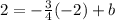
solve for b
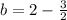
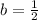
therefore