Question

A friend asks you to borrow $.01 the first day, $.02 the second day, $.04 the third day, $.08 the fourth day, and so on for 15 days. What is the total amount of this request?

Answer 1

The total amount of this request is $ 327.67

Solution:

Given that,

A friend asks you to borrow $.01 the first day, $.02 the second day, $.04 the third day, $.08 the fourth day, and so on for 15 days

Therefore, a sequence is formed as:

0.01, 0.02, 0.04, 0.08 , ....

Let us find the common ratio between terms

`r = (0.02)/(0.01) = 2\\\\r = (0.04)/(0.02) = 2\\\\r = (0.08)/(0.04) = 2`

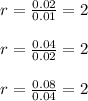
Thus the common ratio is constant

This forms a geometric sequence

The formula to find the first n terms of geometric sequence is:

`S_n = (a_1(1-r^n))/(1-r)`

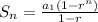
Where,

r is the common ratio,
`r\\eq 1`

`S_n = sum\\\\a_1 = first\ term\\\\n = number\ of\ terms`

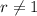
Here in 0.01, 0.02, 0.04, 0.08 , ....

So on for 15 days

`a_1 = 0.01\\\\r = 2\\\\n = 15`

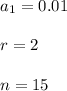
Thus the sum is:

`S_(15) = (0.01(1-2^(15)))/(1-2)\\\\S_(15) = (0.01(1-32768))/(-1)\\\\S_(15) = 0.01 * 32767\\\\S_(15) = 327.67`

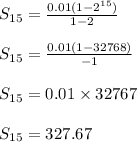
Thus total amount of this request is $ 327.67