Question

You have $7000 with which to build a rectangular enclosure with fencing. The fencing material costs $30 per meter. You also want to have two partitions across the width of the enclosure, so that there will be three separated spaces in the enclosure. The material for the partitions costs $25 per meter. What is the maximum area you can achieve for the enclosure

Answer 1

1857.12 square meters

Explanation:

Let L be the length of the rectangle and 'W' be the width

Perimeter =
`2L + 2W + 2W`

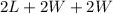
The fencing material costs $30 per meter.

The material for the partitions costs $25 per meter

`cost=30(2L + 2W) +25( 2W)\\60L+60W+50W\\60L +110W`

`7000=60L+110W`

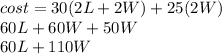
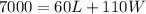
Solve for L

`7000=60L+110W\\7000-110W= 60L\\L=(700)/(6) -(11)/(6) W`

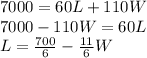
Area = length times width

`( (700)/(6) -(11)/(6) W)(W)\\A(W)=(700)/(6)W -(11)/(6) W^2`

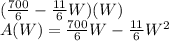
Now take derivative and set it =0

`A(W)=(700)/(6)W -(11)/(6) W^2\\A'(W)=(700)/(6) -(22)/(6) W`

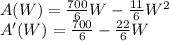
set the derivative =0 and solve for W

`0=(700)/(6) -(22)/(6) W\\(700)/(6)=(22)/(6) W\\W= 31.8`

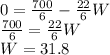
So width = 31.8 that gives maximum area

`L=(700)/(6) -(11)/(6) (31.8)=58.4`

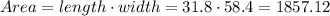`Area = length \cdot width = 31.8 \cdot 58.4= 1857.12` square meter