Answer:
12.66 times the original value.
Step-by-step explanation:
Using the Coulomb's law that states that "the force of attraction or repulsion exerted between two point charges is directly proportional to the product of their magnitudes and inversely proportional to the square of the distance between these charges."
As stated in the law,
The force of repulsion (F) between two point charges is inversely proportional to the distance (r) between these two charges. This means that as the distance increases, the force will decrease and vice versa. i.e;
F ∝
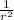
=> F = k /

=> F
 = k
= k
=>
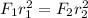 --------------------------(i)
--------------------------(i)
Where;
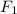 and
and
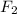 are initial and final magnitudes of the force of repulsion/attraction
are initial and final magnitudes of the force of repulsion/attraction
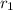 and
and
 are the initial and final distances of separation.
are the initial and final distances of separation.
According to the question,
r has been reduced to 0.281 of the original value. This means that;
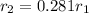
Substituting
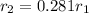 into equation (i) gives;
into equation (i) gives;
=>
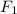 x
x
 =
=
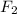 x (0.281
x (0.281
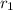 )²
)²
=>
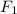 x
x
 =
=
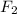 x
x
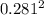 x
x

Dividing both sides by
 to eliminate it, we have;
to eliminate it, we have;
=>
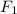 =
=
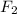 x
x
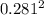
=>
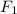 =
=
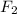 x 0.07896
x 0.07896
Making
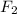 the subject of the formula
the subject of the formula
=>
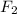 = 12.66 x
= 12.66 x
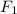 -------------------- (ii)
-------------------- (ii)
From equation (ii),
It is evident that the magnitude of the forces of repulsion has increased to 12.66 times the original value.