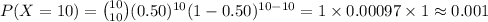Question

List the probability value for each possibility in the binomial experiment calculated at the beginning of this lab, which was calculated with the probability of a success being ½. (Complete sentence not necessary; round your answers to three decimal places) (8 points) P(x=0) P(x=1) P(x=2) P(x=3) P(x=4) P(x=5) P(x=6) P(x=7) P(x=8) P(x=9) P(x=10)

Answer 1

P (X = 0) = 0.001 P (X = 4) = 0.205 P (X = 8) = 0.044

P (X = 1) = 0.010 P (X = 5) = 0.246 P (X = 9) = 0.010

P (X = 2) = 0.044 P (X = 6) = 0.205 P (X = 10) = 0.001

P (X = 3) = 0.117 P (X = 7) = 0.117

Explanation:

In case of a Binomial experiment there are n repeated trials and each trial has only two outcomes: Success or Failure. The probability of success is denoted by p and the probability of failure is (1 - p).

The binomial experiment follows a discrete probability distribution with PDF :

`P(X =x)={n\choose x}p^(x)(1-p^(n-x)`;x = 0, 1, 2, 3...

Given: n = 10 and p = 0.50

(1)

The value of P (X = 0) is:

`P(X =0)={10\choose 0}(0.50)^(0)(1-0.50)^(10-0)=1* 1* 0.00097\approx0.001`

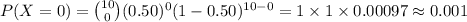
(2)

The value of P (X = 1) is:

`P(X =1)={10\choose 1}(0.50)^(1)(1-0.50)^(10-1)=10* 0.50* 0.00195\approx0.010`

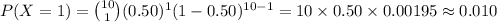
(3)

The value of P (X = 2) is:

`P(X =2)={10\choose 2}(0.50)^(2)(1-0.50)^(10-2)=45* 0.25* 0.00391\approx0.044`

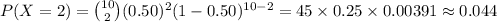
(4)

The value of P (X = 3) is:

`P(X =3)={10\choose 3}(0.50)^(3)(1-0.50)^(10-3)=120* 0.125* 0.007813\approx0.117`

(5)

The value of P (X = 4) is:

`P(X =4)={10\choose 4}(0.50)^(4)(1-0.50)^(10-4)=210* 0.0625* 0.015625\approx0.205`

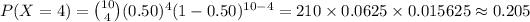
(6)

The value of P (X = 5) is:

`P(X =5)={10\choose 5}(0.50)^(5)(1-0.50)^(10-5)=252* 0.03125* 0.03125\approx0.246`

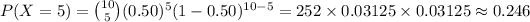
(7)

The value of P (X = 6) is:

`P(X =6)={10\choose 6}(0.50)^(6)(1-0.50)^(10-6)=210* 0.015625* 0.0625\approx0.205`

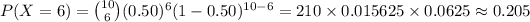
(8)

The value of P (X = 7) is:

`P(X =7)={10\choose 7}(0.50)^(7)(1-0.50)^(10-7)=120* 0.007813* 0.125\approx0.117`

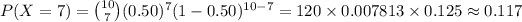
(9)

The value of P (X = 8) is:

`P(X =8)={10\choose 8}(0.50)^(8)(1-0.50)^(10-8)=45* 0.00391* 0.25\approx0.044`

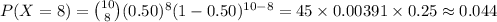
(10)

The value of P (X = 9) is:

`P(X =9)={10\choose 9}(0.50)^(9)(1-0.50)^(10-9)=10* 0.00195* 0.50\approx0.010`

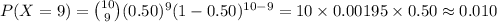
(11)

The value of P (X = 10) is:

`P(X =10)={10\choose 10}(0.50)^(10)(1-0.50)^(10-10)=1* 0.00097* 1\approx0.001`