Part a: -2 is used to eliminate the x-terms when adding with the second equation.
Part b:
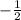 is used to eliminate the x-terms when adding with the second equation.
is used to eliminate the x-terms when adding with the second equation.
Part c:
 is used to eliminate the x-terms when adding with the second equation.
is used to eliminate the x-terms when adding with the second equation.
Part d: 2 is used to eliminate the x-terms when adding with the second equation.
Step-by-step explanation:
Part a: The equations are
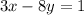 and
and
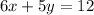
To eliminate the x-terms from both the equations, let us multiply -2 with the first equation and hence it becomes
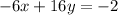
Adding the two equation, we get,
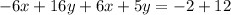
Simplifying, we get,
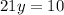
Thus, the x-terms are eliminated when adding the equations.
Hence,-2 is used to eliminate the x-terms when adding with the second equation.
Part b: The equations are
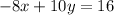 and
and

To eliminate the x-terms from both the equations, let us multiply
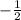 with the first equation and hence it becomes
with the first equation and hence it becomes

Adding the two equation, we get,

Simplifying, we get,
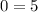
Thus, the x-terms are eliminated when adding the equations.
Hence,
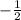 is used to eliminate the x-terms when adding with the second equation.
is used to eliminate the x-terms when adding with the second equation.
Part c: The equations are
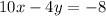 and
and
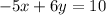
To eliminate the x-terms from both the equations, let us multiply
 with the first equation and hence it becomes
with the first equation and hence it becomes
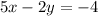
Adding the two equation, we get,
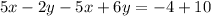
Simplifying, we get,
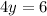
Thus, the x-terms are eliminated when adding the equations.
Hence,
 is used to eliminate the x-terms when adding with the second equation.
is used to eliminate the x-terms when adding with the second equation.
Part d: The equations are
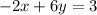 and
and

To eliminate the x-terms from both the equations, let us multiply 2 with the first equation and hence it becomes

Adding the two equation, we get,
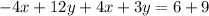
Simplifying, we get,
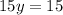
Thus, the x-terms are eliminated when adding the equations.
Hence, 2 is used to eliminate the x-terms when adding with the second equation.