Answer:
maximum height = 80 feet
It reaches maximum height in 2 seconds
Explanation:
A person standing close to the edge on top of a 16-foot building throws a baseball vertically upward.
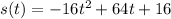
To find maximum height we need to find the vertex
To find x coordinate of vertex use formula
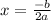
a= -16 , b= 64
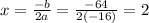
now we plug in 2 for x in s(t) to find maximum height at x=2

so maximum height = 80 feet
It reaches maximum height in 2 seconds