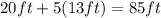Question

The length of the longer leg of a right triangle is

19
ft

more than five times the length of the shorter leg. The length of the hypotenuse is
20
ft

more than five times the length of the shorter leg. Find the side lengths of the triangle.

Answer 1

Answer: The side lengths of the triangle are: 13 (short leg), 85 (hypotenuse), 84 (long leg)

Explanation:

We have a right triangle with the following given lengths:

Shorter leg:
`x`

Longer leg:
`19 ft+5x`

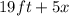
Hypotenuse:
`20 ft+5x`

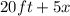
Since this is a right triangle, we can use the Pithagorean theorem:

`(Hypotenuse)^(2)=(Shorter-leg)^(2)+(Longer-leg)^(2)`

`(20 ft+5x)^(2)=x^(2)+(19 ft+5x)^(2)`

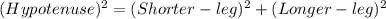
Solving the parenthesis:

`(20 ft)^(2)+(2)(20 ft)(5x)+(5x)^(2)=x^(2)+(19 ft)^(2)+(2)(19 ft)(5x)+(5x)^(2)`

`39 ft^(2)+10 ft x-x^(2)=0`

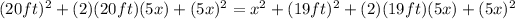
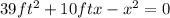
Multiplying the equation by (-1):

`x^(2)-10 ft x-39ft^(2)=0`

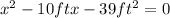
Now we have this quadratic equation, which can be solved with the quadratic formula
`x=\frac{-b\pm\sqrt{b^(2)-4ac}}{2a}`

Where
`a=1`,
`b=-10`,
`c=-39`

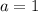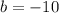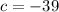
Substituting the known values and choosing the positive result of the equation:

`x=\frac{-(-10)\pm\sqrt{(-10)^(2)-4(1)(-39)}}{2(1)}`

`x=13 ft`

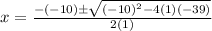
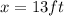
Now we can fin the measure of each leg:

Shorter leg:
`x=13 ft`

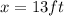
Longer leg:
`19 ft+5(13 ft)=84 ft`

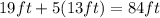
Hypotenuse:
`20 ft+5(13 ft)=85 ft`