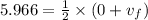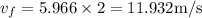Question

To throw the discus, the thrower holds it with a fully outstretched arm. Starting from rest, he begins to turn with a constant angular acceleration, releasing the discus after making one complete revolution. The diameter of the circle in which the discus moves is about 1.9 m?

Answer 1

Complete Question:

To throw the discus, the thrower holds it with a fully outstretched arm. Starting from rest, he begins to turn with a constant angular acceleration, releasing the discus after making one complete revolution. The diameter of the circle in which the discus moves is about 1.9 m.

If the thrower takes 1.0 s to complete one revolution, starting from rest, what will be the speed of the discus at release?

Answer:

11.94 m/s will be the speed of the discus at release.

Step-by-step explanation:

Given data:

Time taken to complete one revolution = 1.0 s

Diameter of the circle, D = 1. 9 m

The radius of the circle is the half of the diameter. So,

`r=(D)/(2)=(1.9)/(2)=0.95 \mathrm{m}`

One revolution is equal to 360 degree or 2 pi or 6.28 radians. Average speed is the ratio of total distance to the time. It can be expressed as

`\text {average speed, } v_(a v)=\frac{\text {total distance}}{\text {total time}}=(2 * \pi * r)/(1)`

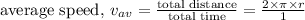
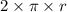`2 * \pi * r` – The distance reached by the thrower to make one revolution

`v_(a v)=2 * 3.14 * 0.95=5.966 \mathrm{m} / \mathrm{s}`

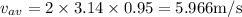
Now, we need to the final velocity (speed of the discus at release). This can be done as below

`v_(a v)=(1)/(2) *\left(v_(i)+v_(f)\right)`

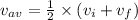
By taking the average of combining both initial and final velocity, we get average velocity. Here, initial velocity is zero.

`5.966=(1)/(2) *\left(0+v_(f)\right)`

`v_(f)=5.966 * 2=11.932 \mathrm{m} / \mathrm{s}`