Question

The table lists pressure and volume values for a particular gas. Which is the best estimate for the value of V at P = 7.0 × 103 pascals?

Answer 1

• 5.4 liters

Step-by-step explanation:

The table with the pressure and volume values for the particular gas of the question is:

P (pascals) V (liters)

5.0 × 10³ 6.0

1.5 × 10⁴ 3.0

2.0 × 10⁴ 2.0

2.5 × 10⁴ 1.5

Since the pressure of 7.0×10³ pascals is between two of the pressures reported in the table, and there is not any simple equation (inverse proportionaliy or a line) that relates those pressures and volumes, you need to interpolate.

Interpolation is calculating an unknown property assuming that the data in between two known set of properties follow a linear relation.

You need to use the points (6.0, 5.0 × 10³) and (3.0, 1.5 × 10⁴), along with (V, 7.0 × 10³)

Where V is the volume that you need to estimate.

The calculation is:

`(V-3.0)/(7.0* 10^3-1.5* 10^4) =(6.0-3.0)/(5.0* 10^3-1.5*10^4)`

`(V-3.0)/(-8000) =(3.0)/(-10000)`

`V=5.4`

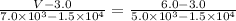
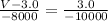
Hence, the best estimate for the value of V at 7.0 × 10³ pascals is 5.5 liters.